COMPUTER SIMULATION OF LOCAL MOBILITY IN DENDRIMERS WITH ASYMMETRIC BRANCHING BY BROWNIAN DYNAMICS METHOD

The Brownian dynamics method has been used to study the effect of the branching asymmetry on the local orientational mobility of segments and bonds in dendrimers in good solvent. “Coarse-grained” models of flexible dendrimers with different branching symmetry but with the same average segment length were considered. The frequency dependences of the rate of the spin-lattice relaxation nuclear magnetic resonance (NMR) [1/T_1H(_H)] for segments or bonds located at different distances from terminal monomers were calculated. After the exclusion of the contribution of the overall dendrimer rotation the position of the maxima of the frequency dependences [1/T_1H(ω_H)] for different segments with the same length doesn’t depend on their location inside a dendrimer both for phantom models and for models with excluded volume interactions. This effect doesn’t depend also on the branching symmetry, but the position of the maximum [1/T_1H(ω_H))] is determined by the segment length. For bonds inside segments the positions of the maximum [1/T_1H(ω_H)] coincide for all models considered. Therefore, the obtained earlier conclusion about the weak influence of the excluded volume interactions on the local dynamics in the flexible symmetric dendrimers can be generalized for dendrimers with an asymmetric branching.

1. Buhleier E., Wehner E., Vogtle F. Cascade-chain-like and nonskid-chainlike syntheses of molecular cavity topologies. Synthesis, 1978, vol. 78, pp. 155–158.
2. Tomalia D.A., Baker H., Dewald J., Hall M., Kallos G., Martin S., Roeck J., Ryder J., Smith P. A new class of polymers: starburst-dendritic macromolecules. Polymer Journal, 1985, vol. 17, pp. 117–132. doi: 10.1295/polymj.17.117
3. Newkome G.R., Yao Z.-Q., Baker G.R., Gupta V.K. Cascade molecules: a new approach to micelles. Journal of Organic Chemistry, 1985, vol. 50, pp. 2003–2004.
4. Dendrimers and Other Dendritic Polymer.Eds. M.J. Frechet, D.A. Tomalia. Wiley, 2001. doi: 10.1002/0470845821
5. Dendrimers in Biomedical Applications. Eds. B. Klajnert, L. Peng, V. Cena. RSC Publishing, 2013, 204 p.
6. Dendrimer-Based Drug Delivery Systems: From Theory to Practice. Eds. Y. Cheng, D.A. Tomalia. Wiley, 2012, 542 p.
7. Polymers and Nanomaterials for Gene Therapy. Ed. R. Narain. Woodhead Publishing, 2016.
8. Patri A.K., Majoros I.J., Baker Jr. J.R. Dendritic polymer macromolecular carriers for drug delivery. Current Opinion in Chemical Biology, 2002, vol. 6, no. 1, pp. 466–471. doi: 10.1016/S1367-5931(02)00347-2
9. Balzani V., Ceroni P., Maestri M., Saudan C., Vicinelli V. Luminescent dendrimers. Recent advances. In: Dendrimers V. Springer, 2003, vol. 228, pp. 159–191. doi: 10.1007/b11010
10. Helms B., Frechet J.M.J. The dendrimer effect in homogeneous catalysis. Advanced Synthesis and Catalysis, 2006, vol. 348, pp. 1125–1148. doi: 10.1002/adsc.200606095
11. Astruc D., Boisselier E., Ornelas C. Dendrimers designed for functions: from physical, photophysical, and supramolecular properties to applications in sensing, catalysis, molecular electronics, photonics, and nanomedicine. Chemical Reviews, 2010, vol. 110, no. 4, pp. 1857–1959. doi: 10.1021/cr900327d
12. Dong R., Zhou Y., Zhu X. Supramolecular dendritic polymers: from synthesis to applications. Accounts of Chemical Research, 2014, vol. 47, no. 7, pp. 2006−2016. doi: 10.1021/ar500057e
13. Stark B., Stuhn B., Frey H., Lach C., Lorenz K., Frick B. Segmental dynamics in dendrimers with perfluorinated end groups: a study using quasielastic neutron scattering. Macromolecules, 1998, vol. 31, no. 16, pp. 5415–5423.
14. Emran S.K., Newkome G.R., Weis C.D., Harmon J.P. Molecular relaxations in ester-terminated, amide-based dendrimers. Journal of Polymer Science, Part B, 1999, vol. 37, pp. 2025–2038.
15. Meltzer A.D., Tirrell D.A., Jones A.A., Inglefield P.T., Hedstrand D.M., Tomalia D.A. Chain dynamics in poly(amido amine) dendrimers. A study of 13C NMR relaxation parameters. Macromolecules, 1992, vol. 25, no. 18, pp. 4541–4548.
16. Meltzer A.D., Tirrell D.A., Jones A.A., Inglefield P.T. Chain dynamics in poly(amido amine) dendrimers. A study of 2H NMR relaxation parameters. Macromolecules, 1992, vol. 25, no. 18, pp. 4549–4552.
17. Aumanen J., Kesti T., Sundstro V., Teobaldi G., Zerbetto F., Werner N., Richardt G., van Heyst J., Vogtle F., Korppi-Tommola J. Internal dynamics and energy transfer in dansylated POPAM dendrimers and their eosin complexes. Journal of Physical Chemistry B, 2010, vol. 114, no. 4, pp. 1548−1558. doi: 10.1021/jp902906q
18. Wittebort R.J., Szabo A. Theory of NMR relaxation in macromolecules: restricted diffusion and jump models for multiple internal rotation in amino acid side chains. Journal of Chemical Physics, 1978, vol. 69, no. 4, pp. 1722–1736.
19. Malveau C., Baille W.E., Zhu X.X., Ford W.T. Molecular dynamics of hydrophilic poly(propylene imine) dendrimers in aqueous solutions by 1H NMR relaxation. Journal of Polymer Science, Part B: Polymer Physics, 2003, vol. 41, no. 22, pp. 2969–2975. doi: 10.1002/polb.10584
20. Markelov D.A., Matveev V.V., Ingman P., Lahderanta E., Boiko N.I. Average relaxation time of internal spectrum for carbosilane dendrimers: nuclear magnetic resonance studies. Journal of Chemical Physics, 2011, vol. 135, no. 12, art. 124901. doi: 10.1063/1.3638177
21. Pinto F., Correa J., Martin-Pastor M., Riguera R., Fernandez-Megia E. The dynamics of dendrimers by NMR relaxation: interpretation pitfalls. Journal of American Chemical Society, 2013, vol. 135, no. 5, pp. 1972–1977. doi: 10.1021/ja311908n
22. Neelov I.M., Markelov D.A., Falkovich S.G., Ilyash M.Yu., Okrugin B.M., Darinskii A.A. Mathematical simulation of lysine dendrimers: temperature dependences. Polymer Science, Series C, 2013, vol. 55, no. 1, pp. 154–161. doi: 10.1134/S1811238213050032
23. Markelov D.A, Falkovich S.G., Neelov I.M., Ilyash M.Yu, .Matveev V.V, Lahderanta E., Ingman P., Darinskii A.A. Molecular dynamics simulation of spin-lattice NMR relaxation in poly-L-lysine dendrimers. Manifestation of the semiflexibility effect. Physical Chemistry and Chemical Physics, 2015, vol. 17, pp. 3214–3226. doi: 10.1039/c4cp04825c
24. Mazo M.A., Shamaev M.Y., Balabaev N.K., Darinskii A.A., Neelov I.M. Conformational mobility of carbosilane dendrimer: molecular dynamics simulation. Physical Chemistry Chemical Physics, 2004, vol. 6, no. 6, pp. 1285–1289.
25. Gurtovenko A.A., Blumen A. Generalized gaussian structures: models for polymer systems with complex topologies. Advances in Polymer Science, 2005, vol. 182, pp. 171–282. doi: 10.1007/b135561
26. Markelov D.A., Lyulin S.V., Gotlib Y.Y., Lyulin A.V., Matveev V.V., Lahderanta E., Darinskii A.A. Orientational mobility and relaxation spectra of dendrimers: theory and computer simulation. Journal of Chemical Physics, 2009, vol. 130, no. 4, art. 044907. doi: 10.1063/1.3063116
27. Markelov D.A., Dolgushev M., Gotlib Y.Y., Blumen A. NMR relaxation of the orientation of single segments in semiflexible dendrimers. Journal of Chemical Physics, 2014, vol. 140, no. 24, art. 244904. doi: 10.1063/1.4884024
28. Roberts B.P., Scanlon M.J., Krippner G.Y., Chalmers D.K. Molecular dynamics of Poly(L-lysine) dendrimers with naphthalene disulfonate caps. Macromolecules, 2009, vol. 42, no. 7, pp. 2775–2783. doi: 10.1021/ma802154e
29. Neelov I., Falkovich S., Markelov D., Paci E., Darinskii A., Tenhu H. Molecular dynamics of lysine dendrimers. Computer simulation and NMR. In: Dendrimers in Biomedical Applications. London, Royal Society of Chemistry, 2013, pp. 99–114. doi: 10.1039/9781849737296-00099
30. Neelov I.M., Janaszewska A., Klajnert B., Bryszewska M., Makova N., Hicks D., Pearson H., Vlasov G.P., Ilyash M.Yu., Vasilev D.S., Dubrovskaya N.M., Tumanova N.L., Zhuravin I.A., Turner A.J., Nalivaeva N.N. Molecular properties of lysine dendrimers and their interactions with αβ-peptides and neuronal cells. Current Medical Chemistry, 2013, vol. 20, no. 1, pp. 134–143. doi: 10.2174/09298673130113
31. Falkovich S., Markelov D., Neelov I., Darinskii A. Are structural properties of dendrimers sensitive to the symmetry of branching? Computer simulation of lysine dendrimers. Journal of Chemical Physics, 2013, vol. 139, no. 7, art. 064903. doi: 10.1063/1.4817337
32. Mikhailov I.V., Darinskii A.A. Does symmetry of branching affect the properties of dendrimers? Polymer Science. Series A, 2014, vol. 56, no. 4, pp. 534–544. doi: 10.1134/S0965545X14040105
33. Simon E.M., Zimm B.H. A computer simulation of the unwinding of a DNA-like helix. Journal of Statistical Physics, 1969, vol. 1, no. 1, pp. 41–55. doi: 10.1007/BF01007240
34. Darinskii A.A., Gotlib Yu.Ya., Lyulin A.V., Neelov I.M. Computer simulation of local dynamics of polymer chain in the orienting field of the LC type. Vysokomoleculyanye Soedineniya, Seriya A, 1991, vol. 33, no. 6, pp. 1211–1220.
35. Darinskii A.A., Lyulin A., Neelov I. Computer simulations of molecular motion in liquid crystals by the method of Brownian dynamics. Macromolecular Theory and Simulations, 1993, vol. 2, pp. 523–530. doi: 10.1002/mats.1993.040020402
36. Neelov I.M., Adolf D.B., Lyulin A.V., Davies G.R. Brownian dynamics simulation of linear polymers under elongational flow: bead-rod model with hydrodynamic interactions. Journal of Chemical Physics, 2002, vol. 117, no. 8, pp. 4030–4041. doi: 10.1063/1.1493187
37. Lyulin A.V., Davies G.R., Adolf D.B. Location of terminal groups of dendrimers: brownian dynamics simulation. Macromolecules, 2000, vol. 33, no. 18, pp. 6899–6900. doi: 10.1021/ma0003811
38. Karatasos K., Adolf D.B., Davies G.R. Statics and dynamics of model dendrimers as studied by molecular dynamics simulations. Journal of Chemical Physics, 2001, vol. 115, no. 11, pp. 5310–5318. doi: 10.1063/1.1394207
39. Neelov I.M., Adolf D.B. Brownian dynamics simulations of dendrimers under elongational flow: bead-rod model with hydrodynamic interactions. Macromolecules, 2003, vol. 36, no. 18, pp. 6914–6924. doi: 10.1021/ma030088b
40. Lyulin S.V., LyulinA.V., Darinskii A.A. Brownian dynamics simulation of charged dendrimers: dynamic properties. Polymer Science. Series A, 2004, vol. 46, no. 2, pp. 196–206.
41. Karatasos K., Lyulin A.V. Local polymer dynamics under strong connectivity constraints: the dendrimer case. Journal of Chemical Physics, 2006, vol. 125, no. 18, art. 184907. doi: 10.1063/1.2386155
42. Neelov I.M., Binder K. Brownian dynamics of grafted polymer brushes. Macromolecular Theory and Simulations, 1995, vol. 4, no. 1, pp. 119–136. doi: 10.1002/mats.1995.040040108
43. Neelov I.M., Binder K. Brownian dynamics of grafted polymer chains: time dependent properties. Macromolecular Theory and Simulations, 1995, vol. 4, no. 6, pp. 1063–1084. doi: 10.1002/mats.1995.040040605
44. Neelov I.M., Borisov O.V., Binder K. Stochastic dynamics simulation of grafted polymer brushes under shear deformation. Macromolecular Theory and Simulations, 1998, vol. 7, no. 1, pp. 141–156.
45. Neelov I.M., Borisov O.V., Binder K. Shear deformation of two interpenetrating polymer brushes. Journal of Chemical Physics, 1998, vol. 108, no. 16, pp. 6973–6988.
46. Sheridan P.F., Adolf D.B., Lyulin A.V., Neelov I.M., Davies G.R. Computer simulation of hyperbranched polymers: the influence of the Wiener index on the intrinsic viscosity and radius of gyration. Journal of Chemical Physics, 2002, vol. 117, no. 16, pp. 7802–7812.
47. Neelov I.M., Adolf D.B. Brownian dynamics simulation of hyperbranched polymers under elongational flow. Journal of Physical Chemistry B, 2004, vol. 108, no. 10, pp. 7627–7636. doi: 10.1021/jp030994q
48. Ermak D.L., McCammon J.A. Brownian dynamics with hydrodynamic interactions. Journal of Chemical Physics, 1978, vol. 69, no. 4, pp. 1352–1360.
49. Voevodin Vl.V., Zhumatii S.A., Sobolev S.I., Antonov A.S., Bryzgalov P.A., Nikitenko D.A., Stefanov K.S., Voevodin Vad.V. Praktika superkomp'yutera "Lomonosov". Otkrytye Sistemy. SUBD, 2012, no. 7, pp. 36–39.

PICTURES

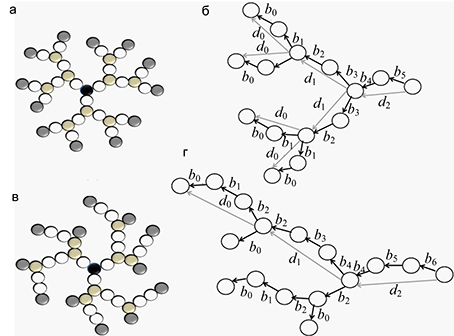
 Fig. 1. Schematic representation of dendrimer models (a), (b) and corresponding branches (b), (g). Symmetrical (a) and asymmetrical (b) dendrimers of the 3rd generation are shown (G=3, where G is the generation number): black, grey and dark grey colors represent the central monomer, branch points and terminal (end) monomers, respectively. The first generation, representing dendrimer core, contains the segments two links in length; in subsequent generations two segments come out of each branch point: two links in length each (a), one link in length and three links in length (c). Schematic representation is given for branches of the symmetric (b) and asymmetric (g) dendrimers. bs  is the vector connecting links in the s-th layer. dmis the vector connecting the segment ends in the m-th layer. The numbering of layers and subgenerations begins with the end groups

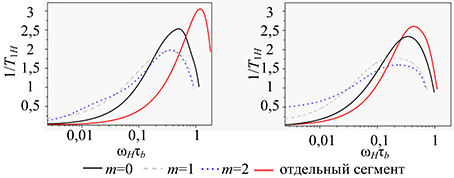
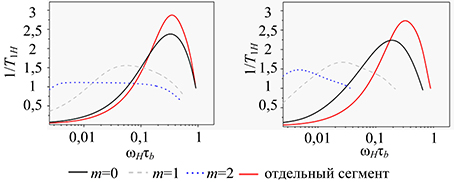
 Fig. 2. The frequency dependences [1/T1H (ωH)]m   forsegments, belonging to different subgenerations mfor symmetrical (a) and asymmetrical (b) phantom model, symmetrical (c) and asymmetrical (g) model  with excluded volume (G=5). For symmetric dendrimers the data is shown for two links segments, for asymmetrical – for three links segments (for asymmetric case the frequency dependence of one link in length segments is shown in Fig. 5). For comparison calculation results are shown for segments of two (a), (b) and three links (b), (g) not included in the dendrimer 

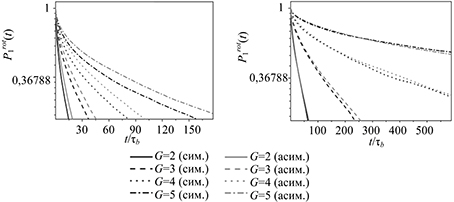
  Fig. 3. Time dependence of the autocorrelation function P1 rot(t) for phantom model (a) and the model with the excluded volume (b)

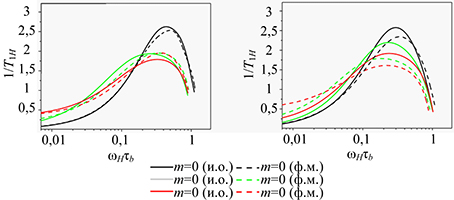
 Fig. 4. The frequency dependences [1/T1H(ωH)]m  obtained after rotation separation as a whole  for segments belonging to different subgenerations m, for the symmetric (a) and asymmetric (b) phantom models (ph.m.) and models with excluded volume (ex. v.) (G=5)

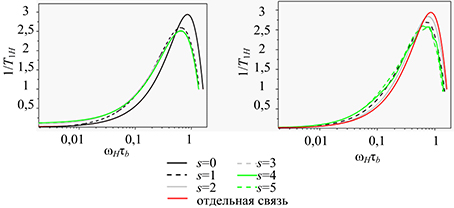
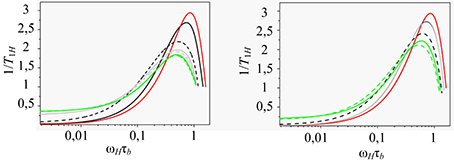
 Fig. 5. The frequency dependences [1/T1H(ωH)]s for the links remoted differently from the end links in dendrimer for symmetric (a) and asymmetric (b) phantom model and symmetric (c) and asymmetric (d) model with excluded volume (G=5). Frequency dependence for separate segment model of two particles connected by a rigid link is also shown

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License